Finding the age by using the angle of the ecliptic
deutsch english español français
Berlin · 2019 Uwe
Topper ![]()
Finding the age by using the angle of the ecliptic
Comments on Dodwell – Richards – Faulkner
Appendix to the article "The diminishing angle of the ecliptic"
and the book "Jahrkreuz" (2016)
Part 1: Shift of the Tropic of Cancer or Change of the Ecliptic ?
The Earth has been regarded as a globe since earliest times. The orb was the hallmark of the globe (in German: ertrike, Earth; see Sachsenspiegel, art. 1, cited in Jung 1939, p. 99). The imperial orb in the emperor's hand could also bear a cross on top (isosceles, but of course without a man attached to it, no cruzifix). This cross was abstract designation of the sun path (4 seasons) as well as the spatial extension of the world (4 directions). The position of the sphere in the wide cosmos served as measure of the passing time.
If Dante could use the lore of an altered position of the Earth regarding the stars by mentioning the Southern Cross as an example in his Divine Comedy (Purgatory 1, as explained in 2007 "Dante - A New Dating"), then this must have accorded with tradition: the position of the Earth in terms of the known constellations must have changed in the past.
It remains unclear whether precession or ecliptic change was considered to be the cause.
This attitude is still practiced today. Both possible causes are used by different archaeoastronomers for age determination. In general, purely mathematical extrapolations based on the balance of forces of the Sun, the Moon and the planets are used both for past precession periods and for the past decrease of epsilon, the ecliptic angle (the earth's axis is straightening up). This resulted in various slightly differing curves with different limits for the cycle.
At times, the rate of change of epsilon of the last two hundred years was also considered and extrapolated for earlier periods, which gave significantly differing curves than the theoretically calculated ones. There are several graphs for the secular change of the obliquity of the ecliptic that differ greatly. (A new one brings Laskar 1986). In addition, an attempt was made to extend historically attested measurements to a millennia-old curve and then to determine the age of buildings by the measured values (e.g. azimuths) they imply. Such a graph deviates noticeably from the theoretically calculated ones (Dodwell, see Part 2).
The immersion of near-horizon constellations by the gradual reduction of the ecliptic angle takes very long time. Due to the precession movement - even more so when this one jumps - a change in the constellations or the pole point would be faster and therefore occur in historical testimonies (like that of Dante).
While the change in the obliquity of the ecliptic has been known for long time, precession has probably been studied and measured only since Hipparchus. Precession's sudden leaps have hitherto scarcely been considered while trying chronological determination.
Summarized here again the basic idea of our theory of precession jumps (as described in 2016 book "Jahrkreuz"):
When a precession jolt occurs, the measurement of times changes; this has the following characteristics:
1. The celestial equator jumps against the ecliptic, shifting the day of the spring equinox on the annual path, which effects the calendar that is moored to the tropical fixed points of the year, e.g. beginning of spring always on March 21 (+ -1), as is the case in our calendar today.
2. The period of circulation (the year length) may change, increase or decrease slightly. The speed of precession can change as a result.
3. The position of the celestial pole shifts.
4. Similarly, the visibility of the stars on the horizon changes.
All those changes happen simultaneously on account of a jolt which then is followed by a swinging movement in both directions ("trepidation"), which will be clearly recognizable for several decades, after that only with good metrology, and later it will no longer be determined.
During such a jolt the geographic north pole (the point where the rotation axis emerges from the globe) does not change.
This principle is always preserved, otherwise the alignment of old solar azimuths or the exact north direction of the Great Pyramid would not be correct today. A wandering of the pole, as assumed by geologists for the history of the Earth, is not feasible in the short period of our tradition.
The mentioned shifts in precession jolts and the continuous straightening up of the ecliptic are not linked to each other, as I have also shown ("Jahrkreuz" 2016, and here: The diminishing angle of the ecliptic.
The change of the date at the jolt (number 1 above) was the reason for the calendar reform of pope Gregor in 1582 (jump over ten days).
The change of the exact year length (above no. 2) has been corrected in the Gregorian calender reform by a new intercalary rule.
The new position of the north pole in the sky (number 3) was of no relevance for the liturgical calendar. It was later made visible in a mosaic in the church of Santa Maria degli Angeli in Rome.
The changes in the visibility of the near-horizon constellations (number 4) play no role in the calendar and therefore have been neglected by the Vatican Commission. They are only of interest today for the purpose of determining the age of prehistoric buildings or documents.
Part 2: Dodwell's Argumentation
Recently, I came across a book on the Internet that deals with the subject of dating using the seculare ecliptic change (not our precession jolts):
Dodwell, George F.: The Obliquity of the Ecliptic. Ancient, medieval, and modern observations of the obliquity of the Ecliptic, in the ancient times and up to the present (Wayville, South Australia, October 1962) Editors: Barry and Helen Setterfield on behalf of the Astronomical Society of South Australia (February 2010).
Dodwell based his theory by criticising Stockwell (1873) and the slightly improved curve by Simon Newcomb 1896. Dodwell found out by 1934 that all early measurements of the ecliptic angle deviated from the "internationally recognized" curve (Stockwell - Newcomb) which was not due to gross errors but to an unknown change in the Earth's movement during that period. The beginning of the drastic change in the ecliptic obliquity for him is at 2345 BC. From then on, there is a constant approximation of the "historically attested" curve of the Earth movement to the logarithmic curve up to 1850 AD, whence the present stability (and final identity of the two curves) is reached.
Contrary to the general view that the earlier measurements testify to the mistakes of the ancient astronomers, Dodwell categorically excludes this (in a submission to the Royal Astronomical Society in 1935, rejected by the latter).
Figure 5:
Dodwell's curve versus the calculated one
(a) From Newcomb's International Formula.
(b) From historical observations gathered by Dodwell.
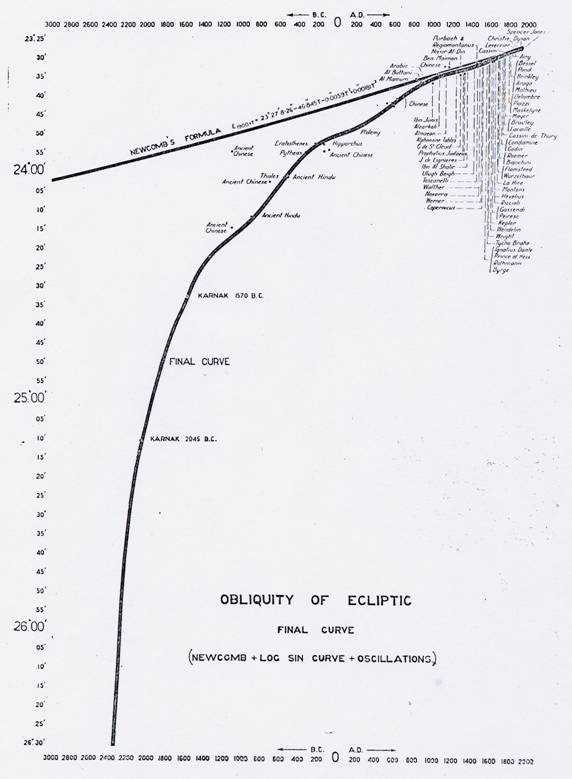
However, Dodwell's "historically documented" data collection and the resulting "final" curve, which he juxtappositions to Newcomb's calculated curve, is questionable. First of all, one notices that the graphs is by no means an ideal curve, but results in an ondulated line. Dodwell always assumed a cyclical precession of around 25,800 years for one cycle.
Dodwell's graph of historical observations is fragile; after 1500 AD it proceeds increasingly weaker back to 1000 AD, then followed by isolated information of the Greeks and, from 0 onward also Chinese, one of them until 1100 BC. A Chinese outlier at 1000 BC is there, too. Then follow two indications for the Egyptian Sun Temple in Karnak, that's it. To interpolate an ideal curve out of those rare points requires skill or generosity.
The selected observations are based on sources whose dating was not critically examined by Dodwell.
Thus, despite all the skepticism and careful exclusion of possible sources of error - such as refraction, blurring shadow boundary or disregard of the difference between the center of the sun and its edge – it never occured to him that the "historical" sources and tacitly incorporated year numbers used by him need have to be subjected to a critical investigation. The year 2345 BC is considered by him the earliest date of ecliptic measurements. Before that, the Earth's axis stood vertically and had been driven into an oblique position due to an abrupt impact.
For this reason, many colleagues rejected the work right then, because the idea of a vertical axis of the Earth is part of the myth of eternal spring and is only a conceived ideal state, which geologists, if at all, relegate to million-year distance.
As far as the sources are concerned, I must point out again that it were the Jesuits who adapted the Chinese texts to the Christian era, with the result that they cannot provide an independant basis in this regard (see Topper, Große Aktion, 1998, Chapter 12). Names like Gaubil, S.J. and Biot, whose works Dodwell used, are to be understood only as support for the Christian chronology. The counterfeiting of the Nestorian stone by Trigault, S. J., who hanged himself after the fraud was discovered, is the most striking example of this mode of operation.
For Hindu measurements, which Dodwell cites, the unreliability of the years is even more pronounced.
The accuracy of the measurements of the ancient Greeks is beyond doubt for Dodwell, which he shows with good arguments. Paul Tannery was one of the few who defended the measurements of Eratosthenes and the other Greeks as exactly, says Dodwell (p. 120). Pythagoras (and his contemporaries such as Thales) had measured virtually exactly 24° for epsilon.
How much the ecliptic has shifted since the Greek Eratosthenes measured it, we can estimate in the situation of Syene, whose well is supposed to have been at 23° 51' 15" N, which agrees with other indications from antiquity, compared to the present latitude 24° 5' 23" N for the same place (Syene, Aswan).
In the summary of chap. 1 Dodwell says: Since the difference of the Newcomb curve from the curve created by observational data since antiquity is not due to measurement errors (as shown), only "the existence of some abnormality of an unexpected kind" can be assumed.
On the other hand: This may refer to the confusion of the chronological benchmarks, for example to a deviation of the mode of counting the years in the individual data, which were not coordinated. Or by retrospective years based on vicious circles (Peiser 1990). Or, for example, by chronological leaps, as they arise from a precession jolt. For this, the ecliptic does not have to change drastically, the distortion in the graph can arise by applying an erroneous chronology.
Part 3: Precursors
The idea that the architects of the Egyptian temples or pyramids might have established an astronomically significant orientation, or even wanted to pass it on, came to the Egyptologists only gradually, but then with undisputed certainty. Using the example of the Sun Temple at Karnak, Norman Lockyer already pointed to the possibility of astronomical age determination. Soon, such alignments were detected at many of the Egyptian temples.
Norman Lockyer wrote in 1894 ("The Dawn of Astronomy") regarding the sun temple at Karnak that the building was aligned very precisely so that the sun's rays were visible on the central altar at sunset on summer solstice. By 18 sight-limiting columns the light beam is narrowed and finally points at the altar.
It is still generally agreed today that the obliquity of the ecliptic applied during the construction of a temple is sufficient if one wants to calculate its date of construction. There was a great outcry when this method was applied to the temple at Karnak which resulted in dates much higher than expected. The archeologists had agreed despite all the imponderabilities on the date 2700 BC. Now Stockwell had calculated for Karnak (with a value of epsilon 24° 12') the enormous age of 7000 BC, while Lockyer got 3700 BC with a slightly gentler curve. There was only one sensible solution to this discrepancy: Contrary to all previous assurances, it was agreed that the sun temple did not indicate any relevant orientation to the sun. The dating on the part of archaeologists had triumphed over that of astronomers.
There is a curious remark to be added: Richards (1921) noticed that the temple axis has a slight bend, which suggests that the sighting angle had changed after construction of the first building, so that the second construction phase used a different azimuth; from this the time interval between the two construction phases might be calculable. Lockyer, however, contented himself with the date of the first building (p. 2). Perhaps the brusque change of the the temple axis could suggest a jerk of the Earth.
(Here are the two temple plans by Richards. On the lower one the bend of the central axis of the building to the left vis-a-vis the main structure is discernible.)
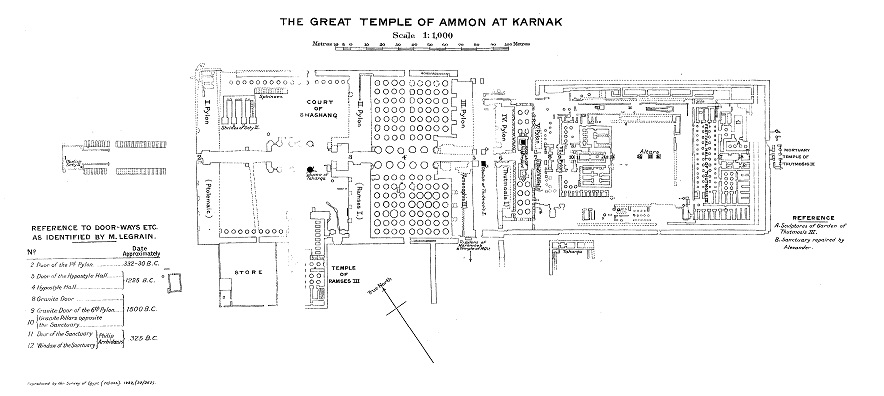
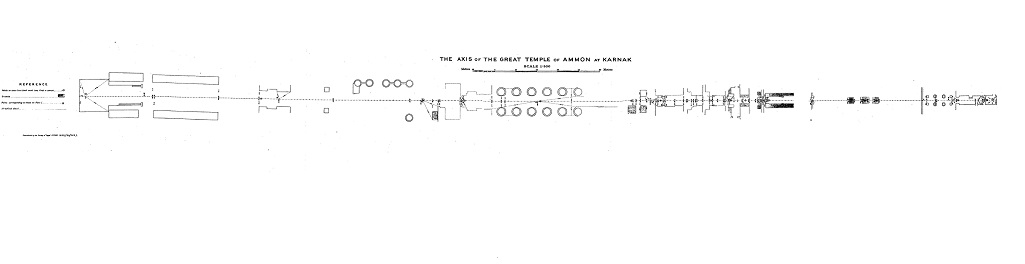
The calculations of Richards and his predecessors are so scrupulously accurate that even minimal factors such as air pressure and temperature were considered for the refraction, as well as the weathering of the column edges (indicated as 1 arcmin in the calculation).
What Richards and Dodwell did not consider: The height or shape of the horizon (and thus the visibility of the sun) could have changed, for example, by tectonic movement.
Richards concludes: Exact astronomical calculations of the ecliptic are scarcely more than 200 years old, and even with the help of traditional eclipses of the last 6,000 years, no exact statement about the ecliptic is possible; therefore relevant dates of the founding of the temple cannot be better than those found by the archaeological research (p. 10).
The result speaks against any astronomical determination of the age of buildings with the help of the respective ecliptic value, as introduced by Lockyer for Stonehenge.
Erich Jung (1939, p. 295) says in the context of solar sighting for the purpose of determining the age of prehistoric constructions that the center of the solar disk has probably been taken, as one would like to infer from the dominant role played by the half sun in German timber construction, e.g. on the decoration of houses, etc. (p. 111).
However, he notes (with reference to Rolf Müller's argumentation) that Lockyer's calculation of the age of Stonehenge using the altered ecliptic angle is uncertain due to the insignificance of the change of epsilon and the inaccuracy of the sighting.
Müller later (1970) based his dating calculations on a theoretical curve of the secular ecliptic change (p. 15 for the period 2000 BC to 2000 AD showing almost a straight line). For 1800 BC, the age most frequently determined by him, he assumed epsilon = 23.9° which, as we learn from Eratosthenes and his predecessors, would have been too small in their day (24°). There are more than 2000 years apart.
Müller (1930) had used a curve of the obliquity of the ecliptic which was proposed by the International Ephemeris Conference in Paris in October 1911, to determine the age of the ruins of the Sun Temple at Tiwanako in Peru. Thereby he obtained unacceptably high values for the Sun Temple which is why he proposed a somewhat narrower curve (Müller fig. 6).
In addition, for the purpose of dating megalithic monuments, Müller has determined the sighting of star risings (p. 137) which can then be applied to the curve of the precession-induced change. The assumption, ascents of stars such as Capella or Wega could have been indicative in the construction of the stone chambers or alignments, however, is completely uncertain and doubted by him.
4. Faulkner's criticism of Dodwell
Dodwell's thesis has recently been taken up by a specialist, Danny Faulkner (2013), who disproves Dodwell and the usefulness of his graph.
Faulkner says: Dodwell quotes several times the Flemish astronomer Godefroy Wendelin, born in 1580, but the more recent data for the obliquity of the ecliptic deviate so little from the Newcomb curve that they fall within the range of inaccuracy. Dodwell "corrected" some of the medieval Arabic data to conform to his curve, who did not "fit" (p. 12).
Faulkner rejects flatly the eleven Chinese statements used by Dodwell (ibid.).
As far as the four Greek data are concerned (fig. 11), their deviation cannot be simply explained by wrong measurement and remain unexplained in the end, but Dodwell's curve is by no means upgraded.
As concerns Dodwell's determination of the ecliptic jolt at 2345 BC, Faulkner explains: Dodwell was a 7-Day Adventist and believed in the creation story, and presumably had calibrated his vertical-axis date on a deluge date from Bishop Ussher (England 1650). That is why Faulkner at the end warns the Creationists, who represent this date, not to rely on Dodwell.
Dodwell was inspired by a book by the Belgian Godfrid Wendelin, which had - after three hundred years of oblivion - reappeared in the library in Brugge and been printed in 1933 in Leuven.
I found it on the internet: Wendelinus, Godefridi (1626): Loxias sev De obliqvitate solis diatriba (Antwerp). It contains information on measurements of epsilon made by the ancient Greeks since Thales of Milet, whom Wendelin locates at 584 BC with epsilon 24° smooth, which makes 20" less after deduction of the solar parallax (in the book of Wendelin p. 18, is a misprint, instead of 29' it must read 59') on the known data of Eratosthenes and Ptolemy (also corrected for parallax), the Arab-Persian Middle Ages (also corrected by 20") to Tycho Brahe and Wendelin's own time (1626). From this amount of dates Wendelin derivates a theory about the change of the ecliptic angle which he calls apocatastasis, restoration. He assumes that 24° 30' is the upper limit, 23° 30' is the lower limit, ie. the diameter is one degree, ie. half a degree each above and below 24°, over a period of 9840 years ending at 1860 AD (thus in the future for Wendelin).
Since Dodwell won his basic information here, his chronological figures are not surprising. An original vertical position of the earth's axis is not mentioned in Wendelin, however.
Faulkner also mentions a recent work on the azimuths of the Egyptian buildings, which examines this theme very decidedly in five chapters: Shaltout and Belmonte, 2005. He notes that none of the Egyptian temples mentions a special solar orientation in their inscriptions.
This study of Belmonte / Shaltout from practically all (around 350) temples and pyramids in Egypt and North Sudan has revealed that their axes coincide frequently on the North Pole, also on the winter solstice, and sometimes on direction east, as well as on star ascents such as Sirius and Canopus. Therefore the astronomical orientation of the buildings was important to the constructors, it was even corrected when the state of the cosmos had changed. Exceptionally, there is also an orientation to the lunar extreme, not targeted from the inside out but vice versa.
What remains is the strange remark that the Egyptians never made precise statements about astronomical sightings; they spoke only of the orientation of the temple by means of a measuring ceremony at the laying of the cornerstone.
Part 5: Hope
Lately, some authors have become a little more cautious with their wording, as far as the stability of precession is concerned, which used to be calculated back over millennia. Dr. Norbert Gasch (Arbeitsgemeinschaft Raumfahrt und Astronomie e.V.) still likes to count many millennia in both directions, but remarks under the heading "precession":
"The period shown here (in 2 figures) covers each 12,000 years in the future and in the past. Going beyond this, possible deviations from the previously known behavior of the Earth's axis are becoming increasingly impracticable and the movement of the stars in the sky becomes ever greater. However, with reserve one can still look further into the future ... Since errors in the self-movement (which changes with time!) and in the precession behavior of the earth are known to pile up the more one moves away from the present, extrapolation is of course not certain indefinitely."
(The unnecessarily complicating mention of the proper motion of the fixed stars I pass over here.)
With regard to the general statement "circle of precession" he says:
"For the northern hemisphere of the Earth there are many simplistic representations in circulation that schematize the precession movement around the pole of the ecliptic as a circle of 23.5 degrees in diameter, but this simplification only partially applies to the true state of affairs, in reality the precession movement describes throughout the millennia a rather complicated rosette line in the sky, as the Earth's axis is also affected by the gravitational fields of the planets."
The two images given there show a precession curve of the northern and southern hemisphere, each an open ellipse with gap at +12900 and -12900 years, which can not be bridged and can be seen rather as a reproduction of a slightly drawn spiral. Bravo!
However, Gasch does not say how this "increasingly unpredictable behavior of the Earth's axis" comes about and how it is recognizable. Whether unacknowledged catastrophes or the chaos theory are up to mischief here?
Until the realization that the curve of the last few millennia of human records reveals gaps in the precession process (Jahrkreuz p. 146, fig. 60), there is still some long way to go.
(For trepidation behavior of the earth due to catastrophic events see also here in the library: Labyrinths - Ritual to overcome Trepidation).
References
Dodwell, George F.: The Obliquity of the Ecliptic. Ancient, mediaeval, and modern observations of the obliquity of the Ecliptic, measuring the inclination of the earth's axis, in ancient times and up to the present (Wayville, South Australia, October 1962 "Manuskript" – edited by Barry und Helen Setterfield im Auftrag der Astronomical Society of South Australia (February 2010)
Faulkner, Danny R. (2013): An Analysis of the Dodwell Hypothesis, in: Answers Reasearch Journal, May 15, 2013 (www.answersresearchjournal.org)
Jung, Erich (2°, 1939): Germanische Götter und Helden in christlicher Zeit (Lehmanns, München-Berlin)
Lockyer, Norman (1894): The Dawn of Astronomy (Cassell, London etc.)
(1909): Surveying for Archaeologists (Macmillan, London)
Müller, Rolf (1930): Der Sonnentempel in den Ruinen von Tihuanacu
(1970): Der Himmel über dem Menschen der Steinzeit (Springer, Berlin-New York)
Newcomb, Simon (1890): Elements of Astronomy (New York)
Peiser, Benny (1990): "Archilochos und Olympia" in: VFG 5/90, S. 20-37 (Mantis, Gräfelfing, in German)
Richards, F. S. (1921): Note on the Age of the Great Tempel of Ammon at Karnak as determined by the Orientation of its Axis (Survey of Egypt Papers, No. 38, Cairo)
Shaltout, M. and J. A. Belmonte (2005): On the orientation of ancient Egyptian temples: (1) Upper Egypt and Lower Nubia. Journal for the History of Astronomy 36, no. 3: 273–298 (Cairo)
Stockwell, John N. (1873): Smithsonian Contributions to Knowledge (USA)
Tannery, Paul (1893): Recherches sur l'histoire de l'astronomie ancienne (Paris)
Topper, Uwe (1998): Die Große Aktion (Grabert, Tübingen)
(2016): Das Jahrkreuz. Sprünge im Verlauf der Zeit (Hohenrain, Tübingen)
(Okt. 2014): The Diminishing obliquity of the Earth
(2008): Cataclysms are the reasons for our wrong chronology (SIS, London)
Uwe Topper, March 28, 2019
![]() I would like to write a comment to this text:
I would like to write a comment to this text: