La disminución de la oblicuidad de la Tierra
aleman inglés español françés
Uwe Topper, Berlin 2018 ![]()
La disminución de la oblicuidad de la Tierra
Parte 1
El nuevo resultado
Hace dos años, en 2016, apareció mi libro "La Cruz del Año Solar: Saltos en la cronología histórica" en alemán (vease noticia aquí) http://www.ilya.it/chrono/sppages/jahrkreuz.html.
Hubo respuestas de respaldo y afirmativas, apenas una crítica dura, como si solo se hubieran expresado cosas bien conocidas u obvias en este libro.
Por supuesto, algunas cosas tienen que ser reexaminadas, pensadas o discutidas. Los "saltos de la precesión" en los cuales el libro se enfoca más que en los previos libros, necesitan ser entendidos antes de que se acepten.
En un punto importante, me desvié de todas las opiniones anteriores: rechazo el supuesto cambio fuerte en la oblicuidad de la órbita de la tierra cuando occurren los llamados saltos de polos.
La oblicuidad de la tierra respeto a su órbita, el ángulo epsilon (ε), está disminuyendo constantemente. Pero si este "movimiento es uniforme durante un largo período, sólo se puede adivinar," digo p. 126. En cualquier caso, rechazo las especulaciones atrevidas de todos los predecesores de que ese ángulo cambie drásticamente a causa de un "salto de los polos". Antiguamente se refirió al modelo mitológico (de autores como Anaxágoras e incluso Heródoto): En la antigüedad el eje de la Tierra era perpendicular a su órbita, entonces no había estaciones, primavera eterna reinaba en nuestras latitudes. Lo repití en 1977 ("La Herencia de los Gigantes"). Ahora, en el capítulo "oposición" (2016, p 266), he dejado claro que considero esta idea ser erronea en lo que concierne los últimos cambios de polos en contra de como lo entienden todos los catastrofistas, sean de los siglos pasados como los de hoy.
Christoph Marx a lo largo de su vida describió esta teoria frecuentemente sostenida por los catastrofistas: que antes del último salto el ángulo epsilon fuese de 32°, en contra de alrededor de 23° 30' que se mide ahora. Concluyó esto a partir de la duración del "año grande" de la precesion que fue de 36.000 años para Hipparco, y ahora está fijada en 25.900 años.
La conclusión es un error, digo en mi libro (2016, p. 268):
"La oblicuidad del tiempo de Ptolomeo fue de 23,9° o de 24°. Transferimos la data al círculo completo de Ptolomeo de 36.000 años, entonces sólo queda una conclusión: la órbita anual de la Tierra (o en la antigua visión: del Sol) debe haber durado alrededor de cinco minutos más que hoy. Fue exactamente este valor el que Hiparco había calculado a partir del movimiento del equinoccio de primavera en el calendario (de 365 ¼ días): se trasladó un día en 300 años, lo que Ptolomeo había confirmado".
La suposición de grandes saltos de la oblicuidad de la eclíptica durante tiempos históricos resulta, por lo tanto, errónea. Para verificarlo consideré los astrónomos de escritura árabes como Albatenio, que habían medido el año trópico con dos minutos de duración menos, mientras que la oblicuidad siguió disminuyendo ligeramente en su tiempo. Por lo tanto, no existe una dependencia directa entre los dos valores (longitud del año y épsilon).
Conclusión: "El salto de la precesión definido por nosotros no conduce a un gran cambio repentino en la oblicuidad, pero a lo sumo una ligera erección de la tierra por unos pocos minutos de arco. En general, epsilon ha cambiado poco en los últimos siglos, independientemente de cambios de la precesión." (2016, p.288).
Esta conclusión se basa en los valores astronómicos tradicionales y es coherente con la situación actual (refiero al libro de texto de Julius Dick). En la "Cruz del Año Solar", subrayo este hallazgo varias veces, y finalmente, en el capítulo "proyecto" (2016, p 444), una vez más destacadamente.
En la descripción del modelo de saltos de precesión (2016, p.147), digo claramente:
"La posición que forma el eje de la Tierra con su órbita, el ángulo de la eclíptica, no cambia en esencial – salvo unas mínimas fluctuaciones deben ser aceptados ..."
La duración del año tropical a veces bruscamente disminuyó considerablemente mientras epsilon no se veia afectado, sino que padece aproximadamente el mismo grado de reducción en todo el tiempo.
Ahora me gustaría explicar este hallazgo un poco más detalladamente, porque la siguiente falacia todavía persigue en los métodos de datación de los arqueoastrónomos:
Debido a que "en los últimos 6.000 años" (Wikipedia) la disminución de la oblicuidad de la eclíptica es de forma continua, resulta bastante simple determinar la edad de un edificio o un texto astronómico si contiene la indicación precisa del ángulo epsilon (ε) directamente o incluida: Se aplica la curva de la variación de épsilon actual y obtiene la diferencia de tiempo que ha pasado hasta el ahora.
Parte 2
El problema de medición, considerado al ejemplo de latitud de lugares en la antigüedad
Al considerar los valores clásicos de la latitud norte de muchas ciudades del mundo habitado (el oikomene), como de Ptolomeo (Geografike, escrita alrededor de "140 dC.") o de sus predecesores, especialmente Estrabón y Plinio, e Hiparco, se nota que los datos son de fiabilidad variable. La gran mayoría de los valores se calculaban, no se midian en el lugar mismo con ayuda del sol o de las estrellas, sino fueron calculadas de acuerdo con la longitud del día en el solsticio de verano en relación con la noche, además por simplicidad en escala de cuartos de horas de diferencia, dando como resultados valores redondeados. En Ptolomeo (Sintaxis), los valores de latitud aparecen en distancias de 5 minutos de arco.
Los pocos datos observados (véase n. 1) están de buen acuerdo, pero todos son más altos por 10 a 20 minutos de arco. Se concluye (Peschel 1877, p. 43) que este se generó a causa de un error sistemático por referirse con el gnomon al borde superior del sol (su sombra), no el centro del sol, lo que hace que sean mayor por hasta 16 minutos de arco (ver fig. 1). La refracción atmosférica puede reforzar este resultado por tan solo un minuto de arco, ya que se mide el ángulo cuando el sol está en su punto más alto, mientras cuando esté en el horizonte el aumento sería considerable según la humedad predominante.
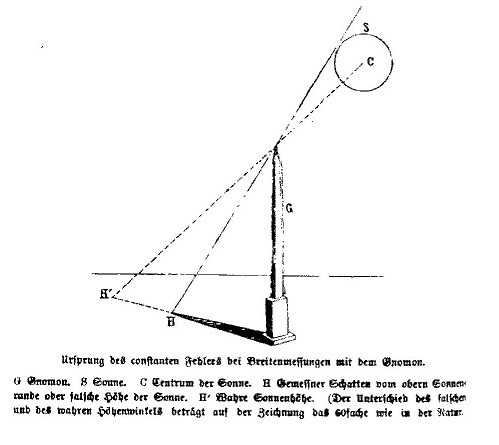
Fig. 1 según Peschel p. 44
Contra la acusación de un error sistemático en la lectura a causa de los astrónomos de la antigüedad, que es reconocido por todos los actuales eruditos de la historia de la astronomía, profiero una objeción: Pusieron de manera intencionada un balón en el obelisco (el gnomon) y luego le toparon con una pequeña cruz o un pico para que el error de lectura se podia evitar. Una mirada a través de un agujero en la piedra evita el mismo error. Ambos artilugios están conocidos desde la antigüedad.
Los valores de los geógrafos antiguos "demasiado altos" para épsilon podrían justificarse.
Al menos, esta afirmación sigue justo: Eratóstenes midió un ángulo mayor de epsilon cuando, por extrapolaciones actuales, debe haber medido menor: Midió 23° 51' 20". ¿Por qué?
Para responder a esta pregunta, hay tres modos de aplicación (véase también n. 2):
1) ¿Por qué Eratóstenes fue incapaz?
2) Eratóstenes no podía estar equivocado;
a) sea que el intervalo de tiempo corrido era mayor que las indicaciones históricas, o
b) que las proyecciones actuales del algoritmo de epsilon deben estar equivocadas.
Se trata del desplazamiento del eje de la Tierra, la reducción de epsilon, la inclinación del ecuador de la Tierra respeto a su órbita. Esta disminución de épsilon se calcula por medio de una fórmula moderna en relación con el tiempo, lo que indica que los valores medidos por los antiguos astrónomos son demasiado altos.
Pero si iban a estar justo? Entonces, la disminución de epsilon en el pasado habría acaecido más rápidamente que asumimos hoy.
Años atrás, esta respuesta me parecía ser la mejor explicación; no importaba para los saltos de precesión proyectados para mi, de lo hice hincapié en el año 2016: la tendencia de cambio es demasiado pequeño para implicar unos notables defectos de las fechas.
En contraste destaca: Los valores de fechación astronómica de los monumentos megalíticos producidos por los arqueologos que resultan milenios superior de lo habitual, me parecen poco fiables debido a la inexactitud de esta calculación. Por lo menos hay que tomar en consideración lo que Peschel observó a este respecto.
Parte 3
Resultado
El algoritmo de recálculo actual indica que la variación de la eclíptica es cíclica durante un período de alrededor de 40.000 años, i.e. que volverá a un valor similar dentro de 40.000 años. La curva parabólica descendente o ascendente lleva unos 20.000 años. En un gráfico (según Laskar 1986, ver n. 3) que refleja el resultado de la extrapolación de los datos actuales de medición y la influencia calculada de los planetas con base de la teoría de la relatividad, se puede juzgar fácilmente que la oblicuidad se redujo constantemente durante los últimos 8.000 años, y que anteriormente augmentaba. Alrededor de 6.000 aC, epsilon fue de 24° 12'. El punto alcanzado alrededor de 3.000 aC. fue 24°. Como la curva no cambia abruptamente sino mas bien sinusoidalmente, el aumento y la disminución en sus puntos de inflexión son muy paulatino. Ahora estamos en el medio de la curva descendente, que es casi rectilinear desde 4.000 antes de hoy (BP) hasta 3.000 después de hoy. Continuará disminuyendo durante unos miles de años, hasta 22° 30', luego aumentará gradualmente de nuevo.
Por suposición convencional, Eratóstenes floreció alrededor de 2.200 antes de hoy. De acuerdo con la curva moderna, el tenía que medir epsilon alrededor de 23° 43', o sea aproximadamente 8' menos que la medida que el logró (23° 51' 20"). Si hubo tiempo vacio (nuestra teoria), su fecha se acerca a nosotros. Reduciendo un milenio, Eratóstenes tenia que medir 23° 36', es decir, 15' menos (un cuarto de grado).
Presumiblemente, los saltos de precesión habrán causado cambios muy pequeños en epsilon, pero cuidado: pequeños. Las estaciones del año habrán cambiados por la reducción de la eclíptica por unos pocos minutos de arco, ya que la diferencia entre 24° 5' (= 24 1/12) (n. 4) y 23° 50' importa a sólo 15 minutos de arco, que corresponde a la diferencia calculada moderna entre hoy y el Imperio Romano. Saltos de precesión y fenómenos similares en otros planetas que influyen sobre epsilon pueden explicar los resultados de medición de Eratóstenes. La naturaleza hace saltos, y la eclíptica lo hace igualmente aunque en medida muy pequeña, no significativa para nosotros.
La pregunta era: ¿Las extrapolaciones de la situación actual son equivocadas porque requieren una excesiva regularidad de movimiento de la Tierra (y del sistema solar en general)? o ¿son inválidas a causa de que el tiempo histórico no se evaluó correctamente, de modo que las fechas proyectadas son correctas para otra escala cronológica?
Para llevar a Eratóstenes en concordancia con los valores extrapolados, tendría que haber vivido anteriormente, mucho más tiempo de lo aceptado. Una reducción del tiempo pasado (nuestra tesis) resultaría en que el momento atribuido a Eratóstenes se proyectaria a un pasado muy lejano. Eso definitivamente alteraría nuestra visión de la historia.
Si a esto no queremos aceptar, entonces la falla no se encuentra en la escala de tiempo histórico (la cronologia tradicional), sino en la adopción de un continuo movimiento de los cuerpos celestes. Incluso en vida de Copernico (es decir, 500 BP) la curva de Laskar desvía ligeramente (es allí más empinada). Copérnico media a epsilon de 23° 28', mientras que del esquema de Laskar se obtiene 23° 30' 20" que indica 2' más. Laskar no se molesta de documentos históricos, mientras digo con Copérnico (2016, p 205): Quién no toma en cuenta los históricamente conocidos cambios caóticos (saltos etc.) observados en el cosmos, persigue una imagen puramente teórico del pasado, sin ninguna pretensión de la realidad.
Es concebible que epsilon bruscamente disminuyó a causa de un salto de precesión por unos pocos minutos de arco, pero luego continúa a disminuir de nuevo por aproximadamente la velocidad usual. La curva no debe haber sido mucho más pronunciada, sólo tiene que haber sido interrumpido. Incluso se puede más o menos derivar la correspondiente disminución de la velocidad suponiendo esta una constante (que es una suposición arbitraria pero posible), y calcular el número de minutos de arco que epsilon habra cambiado en cada uno de los últimos saltos.
Bibliografia
Copérnicus, Nicolaus (1543): Opus de revolutionibus caelestibus (Berlin 1944)
Dick, Julius (1965): Grundtatsachen der sphärischen Astronomie (Leipzig)
Mžik, Hans von (1938): Theorie und Grundlagen der darstellenden Erdkunde (Geografike des Ptolemaios) unter Mitarbeit von Friedrich Hopfner (Gerold, Wien)
Peschel, O. (1877): Geschichte der Erdkunde, 2.ed. (München)
Ptolemäus Sintaxis - Manitius, Karl (1912-13): Des Claudius Ptolemäus Handbuch der Astronomie (Teubner, Leipzig, 2 vol., trad. del griego al alemán, reprint 1963)
Vitruv (1908): Diez libros sobre arquitectura, trad. al alemán par Dr. Franz Reber (Berlin; Wiesbaden 2004)
Notas
1)
Peschel 1877, p. 45:
Eratósthenes (en Strabon) menciona para Alejandria 30° 58' (en vez de: 31° 11') – 13' más alta
Hipparco tiene para Rodos 60 : 43 5/6 = 36° 8' 7" (en vez de 36° 25') – 17' más alta
Pitheas da para Marsilia 42° 57' (en vez de 43° 17' 47") – 20' más alta
para Canopus se da: 31° 5' (en vez de 31° 19' 14") – 14' más alta
Peschel quiere demostrar que los valores antiguos siempre son alrededor de 16' más bajos, porque solo se utilizó el borde superior del sol, i.e. que el centro del sol en el solsticio de verano es más bajo de lo que indica el borde superior de la sombra (le trae un dibujo p. 44, aquí fig. 1)
Vitruv, De architectura IX:
Rom 8:9 = 0,888 = 41° 35' – der genaue Wert heute ist 41° 53' 30" (18' höher)
Athen 3:4 = 0,75 = 36° 55' – genau: 37° 59' (64' höher)
Rhodos 5:7 = 0,714 = 35° 32' , genau 36° 11' (39' höher)
Tarent 9:11 = 0,82 = 39° 20', genau 40° 24' (64' höher)
Alexandria 3:5 = 0,6 = 31° , genau 31° 12' 20" (12' höher)
Por el hecho de que las fracciones deben ser formuladas por números enteras pequeñas y geométricamente expresables, los resultados son bastante buenos. Todos los valores modernos son, por lo tanto, más altos (dos incluso más de 1°).
Si la latitud phi (ɸ) es demasiado baja, epsilon (ε) ha sido mayor.
2) También hay otras respuestas posibles: por ejemplo, la referencia a la deriva de los continentes; o un cambio real del polo (que rechazo para el corto período considerado aquí), o errores de cálculo rectificados aleatoriamente (¡eso también!).
3) ref. Laskar (según wikipedia anglés):
"Durante los últimos 5 millones de años, la oblicuidad de la Tierra ha variado entre 22° 2' 33" y 24° 30' 16", con un período medio de 41.040 años. Este ciclo es una combinación de precesión y el término más grande en el movimiento de la eclíptica. Durante el próximo millón de años, el ciclo llevará la oblicuidad entre 22° 13' 44" y 24° 20' 50"."
"La Luna tiene un efecto estabilizador en la oblicuidad de la Tierra. El análisis del mapa de frecuencias realizado en 1993 sugirió que, en ausencia de la Luna, la oblicuidad puede cambiar rápidamente debido a las resonancias orbitales y el comportamiento caótico del Sistema Solar, llegando a 90° en tan solo unos pocos millones de años."
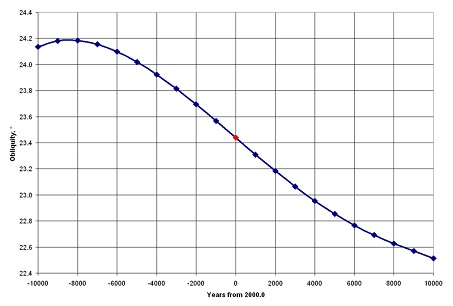
fig. 2: Laskar 1986
4) El valor del ángulo de la oblicuidad (ε) en el momento de Eratóstenes, como se supone que él mismo lo calculó, era la mitad de 11/83 del círculo completo, es decir, 23° 51' 20". El ángulo del trópico de Cancer (en el lugar Syene, hoy Asuan), utilizado para su cálculo del tamaño de la tierra, era un poco más de 24°, exactamente 24° 5' (= 24 1/12). La segunda afirmación probablemente no fue medida por el mismo Eratóstenes, sino provenía de una antigüedad lejana.
Wikipedia continúa: "Ya en el siglo V aC, Oynópides había dado la altitud de Chios como 24°". Entiendo eso, porque él estaba muy anterior de Eratóstenes, por lo que epsilon estaba más cerca de los 24°.
Uwe Topper con la cooperación de Ilya Topper, avril 2018
![]() Quiero escribir un comentario a este texto:
Quiero escribir un comentario a este texto: